• Drag and Drop

• Keyboarding

• Graph paper with rectangle on it-for display

• Graph paper to hand out to students

• Website from the Annenberg Center, Tile Activity

• Math Problem-to display
  “Robby wants to make a garden that has an area of 12 feet. He does not want rabbits to get into his garden, so he will need to buy some fencing. What is the least amount of fencing that he will need?”

• Phet Website
  http://phet.colorado.edu/sims/html/area-builder/latest/area-builder_en.html

• Exit slip using Go Formative or other resource you use in the classroom.

Activity 1

1. Have students sit with their math partner

2. Display a rectangle on grid paper for the students to view. 

3. Review definitions of perimeter and area using a Turn and Talk.

4.  Ask volunteers to share their thoughts with the class using appropriate Math Talk while discussing perimeter and area. 

5. Display the following problem for the students.

“Robby wants to make a garden that has an area of 12 feet. He does not want rabbits to get into his garden, so he will need to buy some fencing. What is the least amount of fencing that he will need?”

6. Ask the students what kinds of tools might help us in solving this problem. 

7. Tell the students that tools we will be using a website and graph paper to solve our word problem.  

8. Give each student a piece of graph paper so that they can use it to record the solutions as we work through this problem. 

9. Display the Tiling Activity for the students to view.  Ask the students to reread the math problem we are going to solve.   

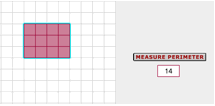
10. On the tiling activity, we will arrange all 12 square tiles on the grid paper to make a rectangle with an area of 12, just like the problem we are solving. Ask students for suggestions about how we could arrange all 12 tiles to make a rectangle. Model this for the students using the display of the Tiling Activity. 

11. Ask a volunteer to tell us the perimeter. 

12. Click on the “Measure Perimeter” button to check their answer.

13. Now  have the students draw this model on their grid paper labeling the area 12 sq units and the perimeter 14 units. When everyone has their model drawn, click the reset button.

 


14. Ask the students if they think there is another way to arrange the 12 tiles into a different shaped rectangle. 
    

15. Now ask a student to use the display to show a second way of arranging the tiles. Check their solution. If correct, have the students record this model on their grid paper, labeling the area and the perimeter. 
    

16. Ask the students to work at their tables to see if there are any other rectangles we could make using all 12 tiles. Ask a volunteer to show the final solution on the display and check their solution with the Measure Perimeter button. 
    

17. Students will label the area and perimeter of the third rectangle.
    

18. Ask the students to look back at the original word problem. Which one do they think Robby should choose in order to buy the least amount of fencing.
    

19. Have students draw a conclusions about the relationship between area and perimeter of the rectangles drawn on the grid paper. (The students should see that  rectangles with the same area can have different perimeters and that the rectangle with a side length of 1 unit, will have the largest perimeter).
    

Activity 2

1. Have students log on to this site, Tiling-Area Builder to access the next activity. This site allows the students to explore area and perimeter using tiling. They can also play a game with different levels to practice making rectangles with certain areas. In the game, the students can choose whether to use a grid or not when modeling and whether or not to have numbers displayed to show the perimeter of the tiles, as well as the perimeter of their model.

2. “Explore” and select the grid and the number tiles in the lower left corner of the screen. Ask them to make a rectangle with an area of 4, dragging tiles from the blue container onto the grid. It will show the students the area and perimeter of the shape. 

3. Ask students to deselect the number and grid options to change the look of the grid.  

4. When ready to move to next task have students select the eraser button to clear their screen. 

Practice Activity

1. Have students working with math buddy or in pairs.

2. Using the PHET website again, have students choose the double grid feature (green and purple) using the button on the right. 

3. Ask the students to make a green rectangle with an area of 14. 

4. Then ask them to make a purple rectangle with an area of 14 that is different than their green rectangle. 

5. Compare the perimeters of the rectangles. 

6. Ask the students if this matches our earlier conclusion about the relationship among the perimeters of the rectangles when the area is the same. Continue with a few more examples discussing their models to prove or disprove the purpose of the lesson.

Students who are in need of more support can work with the teacher in small group while the rest of the students can change to the game and begin completing level 1. 

7. Exit slip using this link at Go Formative with the quick code, HYDQ749.  Students should select “Continue without logging in” The “exit slip” will ask students to  draw 3 different rectangles, each with an area of 18.  They also have one short answer question about the relationship between rectangles with the same area, but different perimeters.

**Go Formative is a student response system that is great for formative assessment. You can create a class and keep track of their progress on the assignments you create or you can make your assignments public, and they can access them using a quick code.

3.MD.D.8   Solve real world and mathematical problems involving perimeters of polygons, including finding the perimeter given the side lengths, finding an unknown side length, and exhibiting rectangles with the same perimeter and different areas or with the same area and different perimeters.

MP2 Reason abstractly and quantitatively

MP3 Construct viable arguments and critique the reasoning of others

MP4 Model with mathematics

Area and Perimeter Practice

Area of Rectangles

Billionaire

Area-Zoo Designer